9. Funções trigonométricas
No círculo trigonométrico temos arcos que realizam
mais de uma volta, considerando que o intervalo do círculo é [0, 2π],
por exemplo, o arco dado pelo número real x = 5π/2, quando desmembrado
temos: x = 5π/2 = 4π/2 + π/2 = 2π + π/2. Note que o arco dá uma volta
completa (2π = 2*180º = 360º), mais um percurso de 1/4 de volta (π/2 =
180º/2 = 90º). Podemos associar o número x = 5π/2 ao ponto P da figura, o
qual é imagem também do número π/2. Existem outros infinitos números
reais maiores que 2π e que possuem a mesma imagem. Observe:
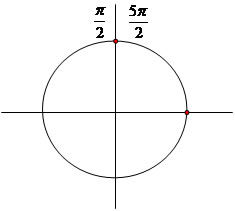
9π/2 = 2 voltas e 1/4 de volta
13π/2 = 3 voltas e 1/4 de volta
17π/2 = 4 voltas e 1/4 de volta
Podemos generalizar e escrever todos os arcos com essa característica na seguinte forma: π/2 + 2kπ, onde k Є Z. E de uma forma geral abrangendo todos os arcos com mais de uma volta, x + 2kπ.
Estes arcos são representados no plano cartesiano através de funções circulares como: função seno, função cosseno e função tangente.
Características da função seno
É uma função f : R → R que associa a cada número real x o seu seno, então f(x) = senx. O sinal da função f(x) = senx é positivo no 1º e 2º quadrantes, e é negativo quando x pertence ao 3º e 4º quadrantes. Observe:
13π/2 = 3 voltas e 1/4 de volta
17π/2 = 4 voltas e 1/4 de volta
Podemos generalizar e escrever todos os arcos com essa característica na seguinte forma: π/2 + 2kπ, onde k Є Z. E de uma forma geral abrangendo todos os arcos com mais de uma volta, x + 2kπ.
Estes arcos são representados no plano cartesiano através de funções circulares como: função seno, função cosseno e função tangente.
Características da função seno
É uma função f : R → R que associa a cada número real x o seu seno, então f(x) = senx. O sinal da função f(x) = senx é positivo no 1º e 2º quadrantes, e é negativo quando x pertence ao 3º e 4º quadrantes. Observe:
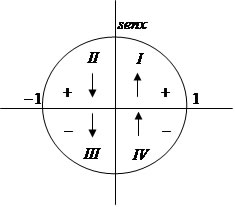
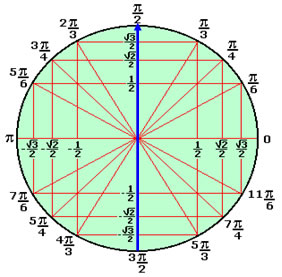
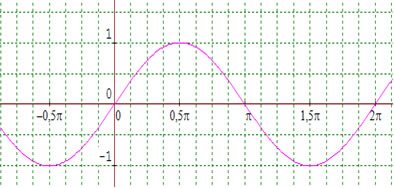
Gráfico da função f(x) = senx
Características da função cosseno
É uma função f : R → R que associa a cada número real x o seu cosseno, então f(x) = cosx. O sinal da função f(x) = cosx é positivo no 1º e 4º quadrantes, e é negativo quando x pertence ao 2º e 3º quadrantes. Observe:
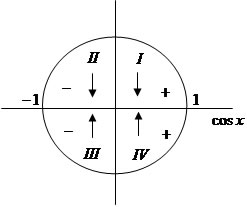
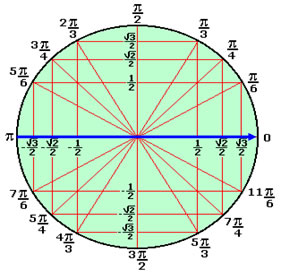
Gráfico da função f(x) = cosx
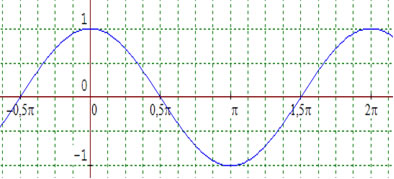
Características da função tangente
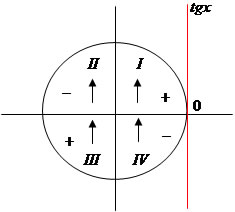
É uma função f : R → R que associa a cada número real x a sua tangente, então f(x) = tgx.
Sinais da função tangente:
É uma função f : R → R que associa a cada número real x a sua tangente, então f(x) = tgx.
Sinais da função tangente:
Valores positivos nos quadrantes ímpares.
Valores negativos nos quadrantes pares.
Crescente em cada valor.
Valores negativos nos quadrantes pares.
Crescente em cada valor.

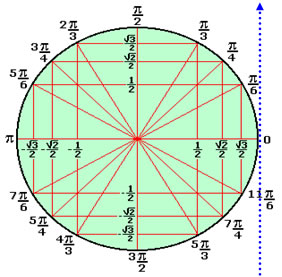
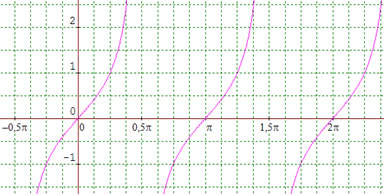
Gráfico da função tangente
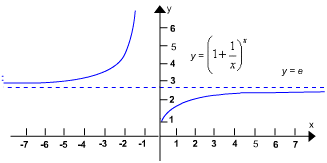
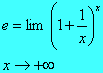 e
e