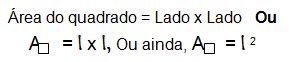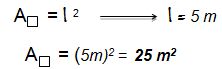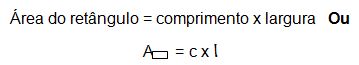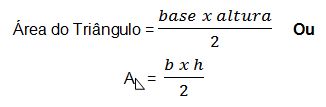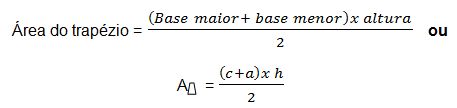6 - Cálculo de áreas nas principais figuras
geométricas
Conhecer sobre área é conhecer sobre o espaço que podemos preencher
em regiões poligonais convexas – qualquer segmento de reta com
extremidades na região só terá pontos pertencentes a esta.

O cálculo de áreas tem muita aplicabilidade em diferentes momentos,
seja em atividades puramente cognitivas, ou até mesmo trabalhistas. Um
exemplo de profissional que faz uso dessa ferramenta para tornar
possível o desempenho do seu trabalho é o pedreiro. É através do
conhecimento de área que é possível estimar a quantidade de cerâmica
necessária para pavimentar um determinado cômodo de uma casa, por
exemplo.
O quadrado
O quadrado é uma figura geométrica plana regular em que todos os seus
lados e ângulos são iguais. Veja um exemplo de quadrado na figura a
seguir:

Para calcular a área de um quadrado basta que se multipliquem dois dos seus lados
l entre si.
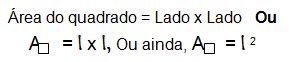 Exemplo 1
Exemplo 1
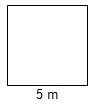
Para pavimentar a sala de sua casa D. Carmem comprou 26 m
2
de piso. Sabendo que a sala tem o formato quadrangular e que um dos
lados mede 5 m, diga se o piso comprado por D. Carmem será suficiente
para pavimentar a sua sala.
- A sala tem o formato quadrangular;
- O seu lado mede 5 m;
- A área do quadrado é A = l 2.
Com base nos dados acima temos:
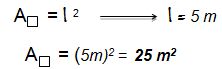 Conclui-se então que o piso comprado por D. Carmem será suficiente para pavimentar sua sala e ainda sobrará 1 m2.
Lembrete: a unidade de medida de área mais utilizada é o metro quadrado (m2), porém em alguns casos usa-se o km2, cm2, etc.
Conclui-se então que o piso comprado por D. Carmem será suficiente para pavimentar sua sala e ainda sobrará 1 m2.
Lembrete: a unidade de medida de área mais utilizada é o metro quadrado (m2), porém em alguns casos usa-se o km2, cm2, etc.
O retângulo
O retângulo é uma figura geométrica plana cujos lados opostos são
paralelos e iguais e todos os ângulos medem 90º. Confiram o retângulo
abaixo:

Para calcular a área do retângulo, basta que se multipliquem seu comprimento
c pela largura
l.
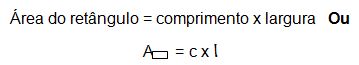 Exemplo 2
Exemplo 2
Num campeonato de futebol a equipe organizadora do evento está
providenciando o gramado que será plantado em toda área do campo. Para
comprar as gramas, a equipe precisa saber a área do campo, pois a grama é
vendida por metro quadrado. Sabendo que o campo tem 115 m de
comprimento por 75 m de largura e ainda que o campo tem o formato
retangular, ajude a equipe a solucionar o problema, diga quantos metros
quadrados de área tem o campo de futebol?

O triângulo
O triângulo é uma figura geométrica plana formada por três lados e três ângulos. A soma dos seus ângulos internos é igual 180º.
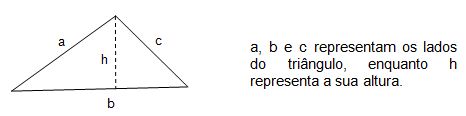
Para calcular a área do triângulo multiplica-se a base
b pela altura
h e divide o resultado por 2 (metade da área do retângulo).
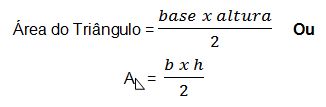 Exemplo 3
Exemplo 3
Encontre a área de um triângulo cuja base mede 8,2 cm e a altura 3,6 cm.

O trapézio
O trapézio é uma figura plana com um par de lados paralelos (bases) e um par de lados concorrentes.

Para calcular a área do trapézio adiciona-se a base maior
c à base menor
a, ao resultado da soma multiplica-se a altura, e por fim, divide-se o resultado final por 2.
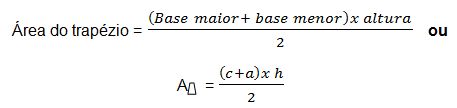 Exemplo 4
Exemplo 4
Um fazendeiro quer saber a área de um lote de terra que acabara de
comprar. O lote tem o formato de um trapézio. Sabendo que a frente mede
1020 m, o fundo, 815 m e a distância da frente ao fundo é de 510 m.
Determine a área do lote.

Conclusão:
A
necessidade geométrica perpassou o tempo e está impregnada em nossas vidas nos
dias atuais. O conhecimento da Geometria Plana (Euclidiana) é tão importante
que não é possível o caminhar separado da sua prática e do seu entendimento.
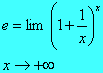 e
e